



无定型药物因为其高能态特性而具有显著优于结晶态药物的溶解度,这一特性使其成为改善难溶性药物递送的重要策略。然而,这种高能态特性也导致了无定型药物在储存过程中的不稳定性,具体表现为有自发结晶倾向,可能影响药物疗效和安全性。
传统观点认为分子动力学是决定无定型药物结晶倾向的主要因素。本研究通过创新性的实验设计和理论建模,颠覆性地揭示了热力学参数(ΔG和ΔS)在结晶过程中的主导作用。通过四种玻璃化转变温度(Tg)相近(45 ºC)但热力学性质各异的模型药物(硝苯地平NFP、吲哚美辛IMC、非洛地平FLP和酮康唑KTZ)的对比,系统探究了无定型药物结晶倾向的调控机制。这一发现不仅深化了对无定型系统相变行为的理论认识,也为制药工业中无定型制剂的设计与开发提供了重要的科学依据。
原文链接:
DOI:10.1021/acs.molpharmaceut.1c00839
分子迁移率对物理稳定性的作用一直是药学领域的研究热点。储存稳定性通常与药物的玻璃化转变温度Tg相关。全局分子迁移率(通常称为α-弛豫)源于长程协同运动,是玻璃化转变的原因。高于Tg时,分子迁移率的增强会促进结晶,如硝苯地平、塞来昔布、桂利嗪和对乙酰氨基酚,其无定型在Tg以上容易结晶。相反的,在Tg下储存,分子迁移率降低,可以使药物保持无定型的状态。而在远低于Tg的温度下储存可以显著降低分子迁移率,从而完全抑制结晶。如塞来昔布,在Tg以上易结晶,但在Tg以下储存数月仍能保持无定型。但并非所有化合物都有相同的表现。硝苯地平和灰黄霉素即使在低于Tg几度的温度下储存,也会在几天内结晶。除了α-弛豫过程外,无定型体系中还可能观察到次级弛豫(β-、γ-、δ-等),并可以通过介电光谱测得。已有许多关于结晶时间与α-弛豫时间在Tg以上耦合的报道。然而,硝苯地平和非洛地平的分子迁移率(α-弛豫)非常相似,但它们的结晶倾向却存在显著差异。显然,分子迁移率并不能完全解释药物的结晶倾向。需要通过同时控制温度和压力保持分子迁移率恒定,来研究热力学参数对结晶倾向的影响。
关于热力学在无定型结晶倾向中的作用,已有一些研究。构型热力学参数,尤其是无定型和晶型之间熵、焓和吉布斯自由能的差异,为结晶的热力学起源提供了衡量标准。在一项研究中,将硝苯地平和利托那韦在低于各自Tg值25 ºC的温度下的结晶行为进行比较,硝苯地平较低的熵势垒和较高的分子迁移率使其具有较高的结晶倾向。通过热分析测量的分子迁移率和构型熵,形成了无定型分类系统发展的基础,以评估药物结晶的风险。但这种分类系统并不能解释结构差异较小的化合物在结晶行为上的显著差异。
时间-温度转变(TTT)图显示了结晶起始的时间和温度依赖性(图1)。其中,温度为时间的函数,这条线是完全无定型相(白色无阴影区域)与包含无定型和晶体相(蓝色阴影区域)之间的相边界。当保持在特定温度时,体系保持在无定型状态,直到达到相边界,对应的时间即为结晶起始时间。当温度介于Tg和Tm(熔点)之间时,结晶诱导时间对温度的依赖性最小。
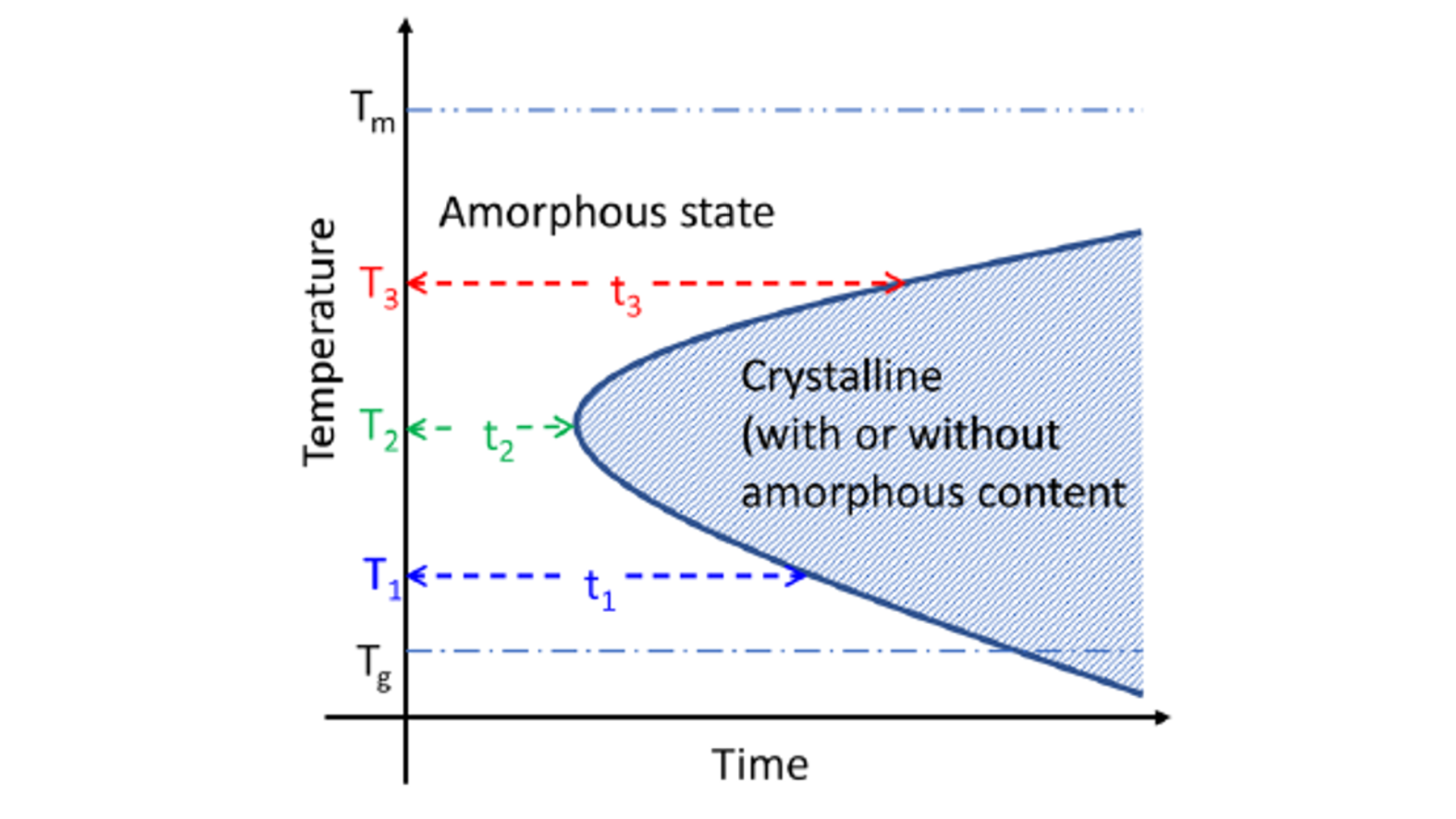
图 1 Schematic representation of the time−temperature-transformation (TTT)
无定型的结晶动力学是由成核速率和晶体生长速率决定的。在接近Tg的温度下,成核速率最大,而在接近Tm的温度下,生长速率可能最高。因此,总体结晶速率会在Tg和Tm之间出现峰值。成核速率是结晶诱导时间的关键决定因素,并受到粘度和成核能垒的调控。
已有研究人员尝试阐明动力学和热力学在无定型药物结晶中的联合作用,并取得了一些成果。然而,尚未有研究阐明动力学和热力学的具体作用。为了使动力学效应最小化,研究团队选择了四种模型药物(硝苯地平NFP、吲哚美辛IMC、非洛地平FLP和酮康唑KTZ)。他们具有几乎相同的Tg(45 ºC),并在相关温度范围内显示出极为相似的分子迁移率,同时在结晶行为上存在显著差异(表1)。这种设计为有机小分子结晶中的动力学和热力学因素的联系提供了途径。
表 1 Relevant Properties of the Different Polymorphic Forms of the Model Compounds

实验方法与技术路线
01 由时间依赖性Cp得到结晶诱导时间
在Tg以上,无定型化合物的比热容(Cp)明显高于其对应的晶型(图2A),并可以通过类等温调制DSC技术测得。结晶起始于Cp的第一个台阶式下降(图2B)。在过冷状态T1、T2和T3三个温度下等温保持,对应的结晶起始时间分别为t1、t2和t3(图2B)。
Cp随时间的变化提供了定量结晶度(xcr)的方法。xcr对于时间的函数可以表示为
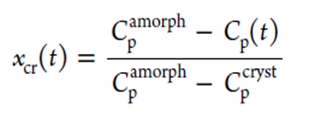
由于不同的晶型应具有非常相似的Cp,因此xcr的值基本与结晶形式无关。这里假定结晶度与比热容成线性正比。广泛用于描述结晶动力学的Johnson-Mehl-Avrami方程
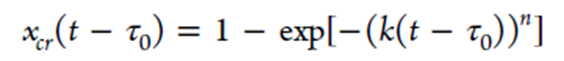
其中τ0为结晶诱导时间,xcr(t - τ0)为(t - τ0)时刻的结晶度,k为反应速率常数,n为Avrami指数。因此,结晶诱导时间是衡量无定型体系物理稳定性的一个指标。

图 2 (A) A schematic representation of the Cp value of a compound in the amorphous and crystalline states as a function of temperature. (B) Isothermal hold leads to crystallization resulting in a decrease in Cp
02 结晶倾向:热力学和动力学
结晶时间是成核时间和能够检测到晶核的生长时间的总和,即为Johnson-Mehl-Avrami方程中的诱导时间τ0,与稳态成核速率成反比。稳态成核速率可表示为
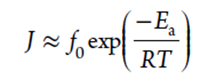
其中T为温度,R为通用气体常数,Ea为成核活化能,f0为分子从亚稳态加入到稳定晶体的“尝试频率”。
成核的驱动力是无定型和晶型之间的自由能差。为了成核,分子必须尝试克服活化能势垒。这些尝试在时间尺度上可以用分子迁移率来描述。单位时间内的尝试次数称为尝试频率,与弛豫时间成反比。因此,尝试频率成为动力学上的驱动力,而活化能是结晶行为的热力学壁垒。
根据经典成核理论,成核是有利的吉布斯自由能(ΔG)和不利的界面表面能(σ)之间的竞争。成核的活化能Ea = 16πσ3/3ΔG2,其中σ为界面表面能,ΔG为晶态和非晶态之间的吉布斯自由能之差。稳定晶核的最小尺寸被称为临界半径rc = 2σ/ΔG。稳态成核速率可表示为
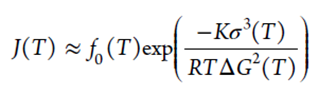
其中K是与成核性质和晶核形状相关的常数。
尝试频率与分子迁移率的时间尺度相关。在无定型体系中,分子迁移率是一种控制结晶的因素。由长程协同运动引起的α-弛豫过程,则是玻璃化转变的原因之一。利用介电光谱(DES)可以得到α-弛豫时间对温度的函数τα(T)。单位时间内成核的尝试频率可表示为α-弛豫时间的倒数:f0(T) = 1/τα(T)。这些尝试中只有一小部分会成功,导致晶核的形成等于或大于临界半径,可称为成功跳跃频率。成功成核事件的次数J(T) = 1/τs(T),其中1/τs(T)即为成功跳跃频率(单位时间内单位体积内成功跳跃的次数)。由此可以得到

因此,成功跳跃频率1/τs(T)是尝试频率1/τα(T)和热力学活化能Ea(T) = K(σ3(T)/ΔG2(T))的函数。ΔG(T)和σ(T)的温度依赖性决定了Ea(T)的温度依赖性。热力学函数ΔG(T)可以从化合物非晶态和晶态的比热容数据中得到。随着σ值的增大,无定型态随着成核活化能的增大而变得更加稳定。在许多化合物中,界面表面能与晶态和非晶态之间的焓差ΔH(T)成正比,可以表示为σ(T) = hΔH(T),其中h为比例常数。其也与界面附近液体分子的有序过程所造成的熵失有关。随着晶态和非晶态之间熵差的增加,形成界面将产生更高的熵“代价”,可表示为

其中A是与温度无关的比例常数。这与观察到的结晶阻力随熵差(ΔS)的增加而增加的现象一致。熵差ΔS可以从非晶态和晶态的比热容数据中得到。因此,成功跳跃频率可以用ΔS和ΔG表示
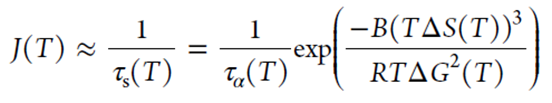
其中B=KA3,是一个与温度无关的无量纲常数。
诱导时间与稳态成核时间成反比,即得1/τ0∝1/τs。因此诱导时间可表示为
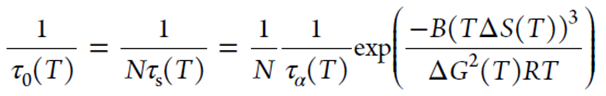
其中N是诱导时间与成核速率的比例常数,可以解释为形成临界密度所需的晶核数的量度。
能量分布图(图3)展示了结晶倾向的热力学和动力学基础。
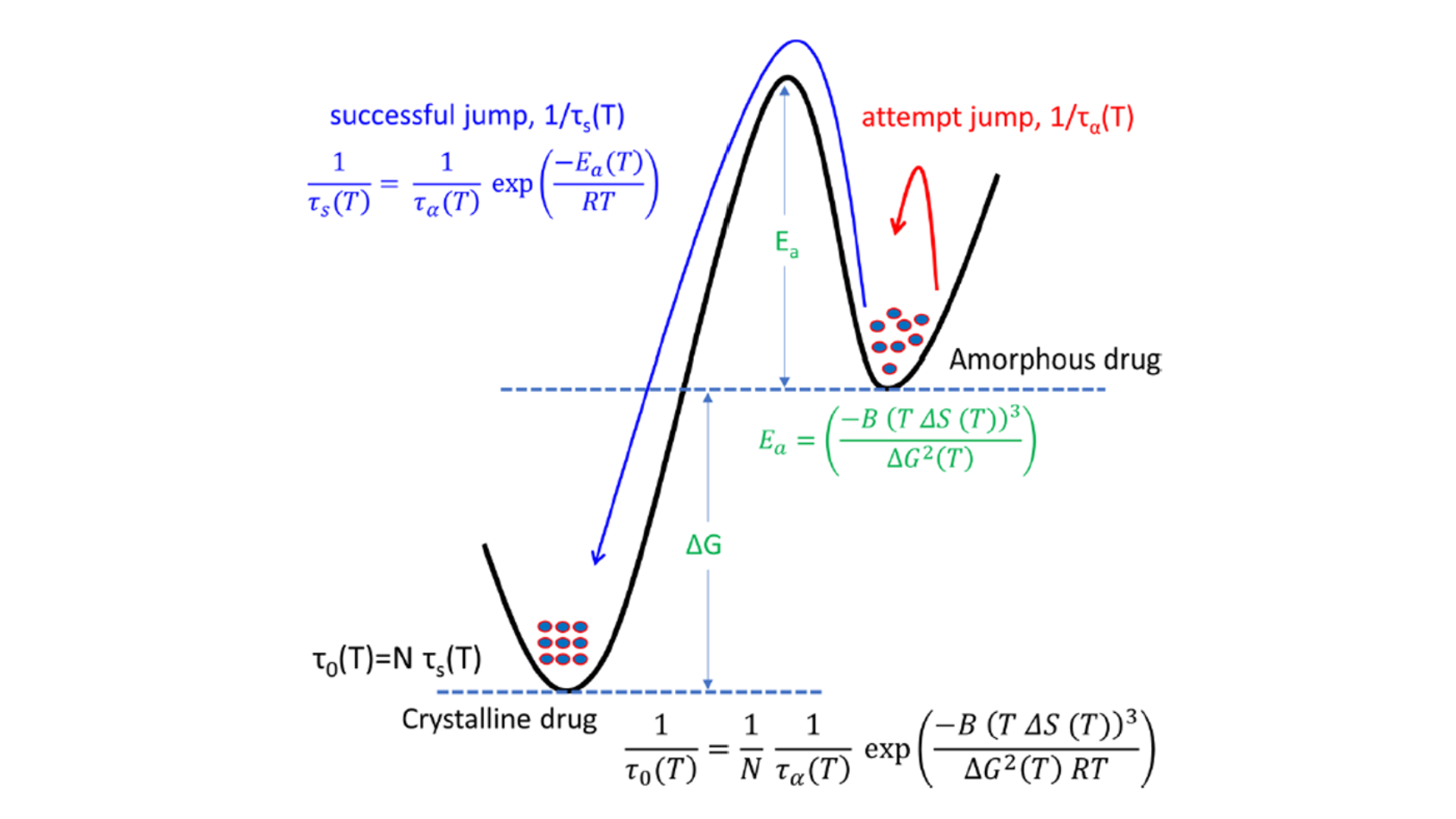
图 3 Schematic of the energy landscape: attempt jump and activation barrier for nucleation.
结果与讨论
01 模型化合物的性质
尽管四种模型化合物有非常相近的Tg,这些化合物在其对应的过冷熔体中的结晶倾向有很大的不同。当快速冷却(冷却速度大于20 ºC/min)时,四个化合物均没有结晶。随后加热时,只有NFP结晶,这反映了其结晶倾向与其他化合物的本质差异。
NFP、IMC和FLP均存在多晶型现象。通过同步辐射鉴定晶型,无定型NFP形成Form I型(α晶型)和Form II(β晶型)的混晶。IMC在90 ºC形成γ晶型外,在其他实验温度下均形成Form II(α晶型)。无定型FLP在60 ºC和70 ºC时形成Form I,在80 ºC时形成Form I和Form II的混晶。
02 模型化合物的时间-温度转变(TTT)
通过由Avrami图得到的诱导时间生成四个模型化合物的TTT图(图4)。四种模型化合物的结晶倾向排序为NFP > IMC > FLP > KTZ。
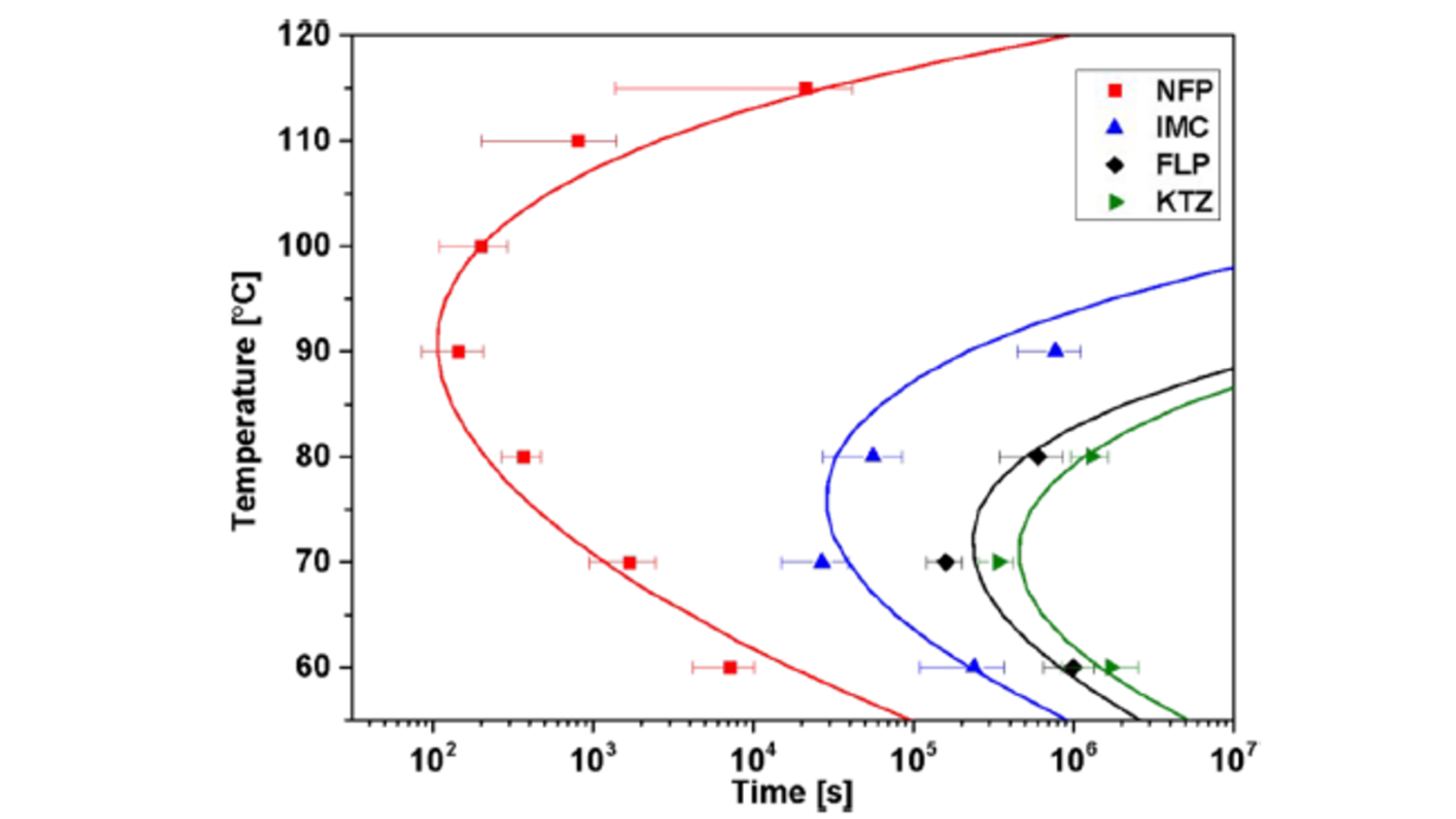
图 4 TTT diagram for the crystallization induction time of the model compounds at different temperatures.
03 模型化合物的分子迁移率
分子迁移率是结晶过程中成核和生长的动力学驱动力。采用介电光谱法测定α-弛豫时间以表征模型化合物的分子迁移率。模型化合物的介电响应作为特定温度下电场频率的函数,可以得到复相对介电常数ε*(ω)。采用Havriliak−Negami函数对介电数据进行分析。
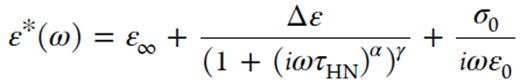
其中ε∞是高频介电常数,ε0是自由空间介电常数,σ0是电导率。Δε是弛豫过程的介电强度,τHN是HN弛豫时间。形状参数α和γ分别表示介质损耗的对称和非对称展宽以及弛豫时间的分布。取系统的平均迁移率为介质损耗峰值对应的弛豫时间,可以表示为

四种模型化合物的弛豫时间曲线表现出相似的温度依赖性,由Vogel-Fulcher-Tammann方程建模:
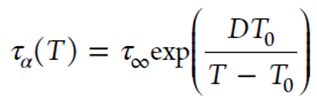
其中,τ∞是“无限”温度下的弛豫时间,T0为零迁移温度,D为常与脆性相关的强度参数。虽然模型化合物的VFT参数不同,但在所研究的温度范围内,四种化合物表现出相似的分子迁移率。
根据与温度无关的VFT参数建立结晶诱导时间,可以表示为
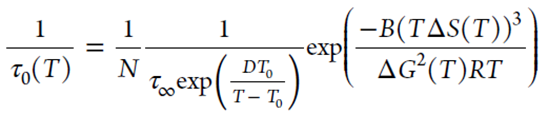
该方程以热力学函数(ΔS和ΔG)以及与温度无关的迁移率参数(D、T0、τ∞)体现了结晶诱导时间的温度依赖性。
四种模型化合物的弛豫时间在很宽的温度范围内是相似的,因此克服成核能垒的尝试跳跃频率并无不同。然而,结晶诱导时间表现出明显的差异。因此,分子迁移率不能单独用来解释这些化合物结晶倾向的差异。
04 模型化合物的构型焓、熵和自由能
构型热力学函数,特别是非晶态和晶态之间的熵、焓和吉布斯自由能的差异,可以从DSC数据中得到。
构型比热容,即化合物的非晶态和晶态之间的热容之差,可以表示为
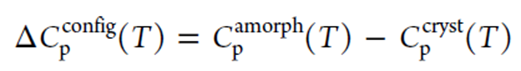
由此可以得到晶态和非晶态之间的焓差ΔH(T)和熵差ΔS(T)对温度的函数

其中T是温度,ΔHm和ΔSm分别是聚变的焓和熵。非晶态和晶态的吉布斯自由能差值ΔG(T) 可以表示为
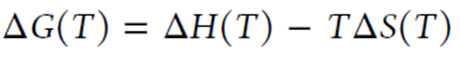
(图5)。
当温度接近Tg时,在大部分温度范围内,模型化合物的ΔG排序为KTZ >NFP>IMC>FLP。因此,自由能驱动力(ΔG)或熵势垒(ΔS)的值与结晶倾向没有直接联系。
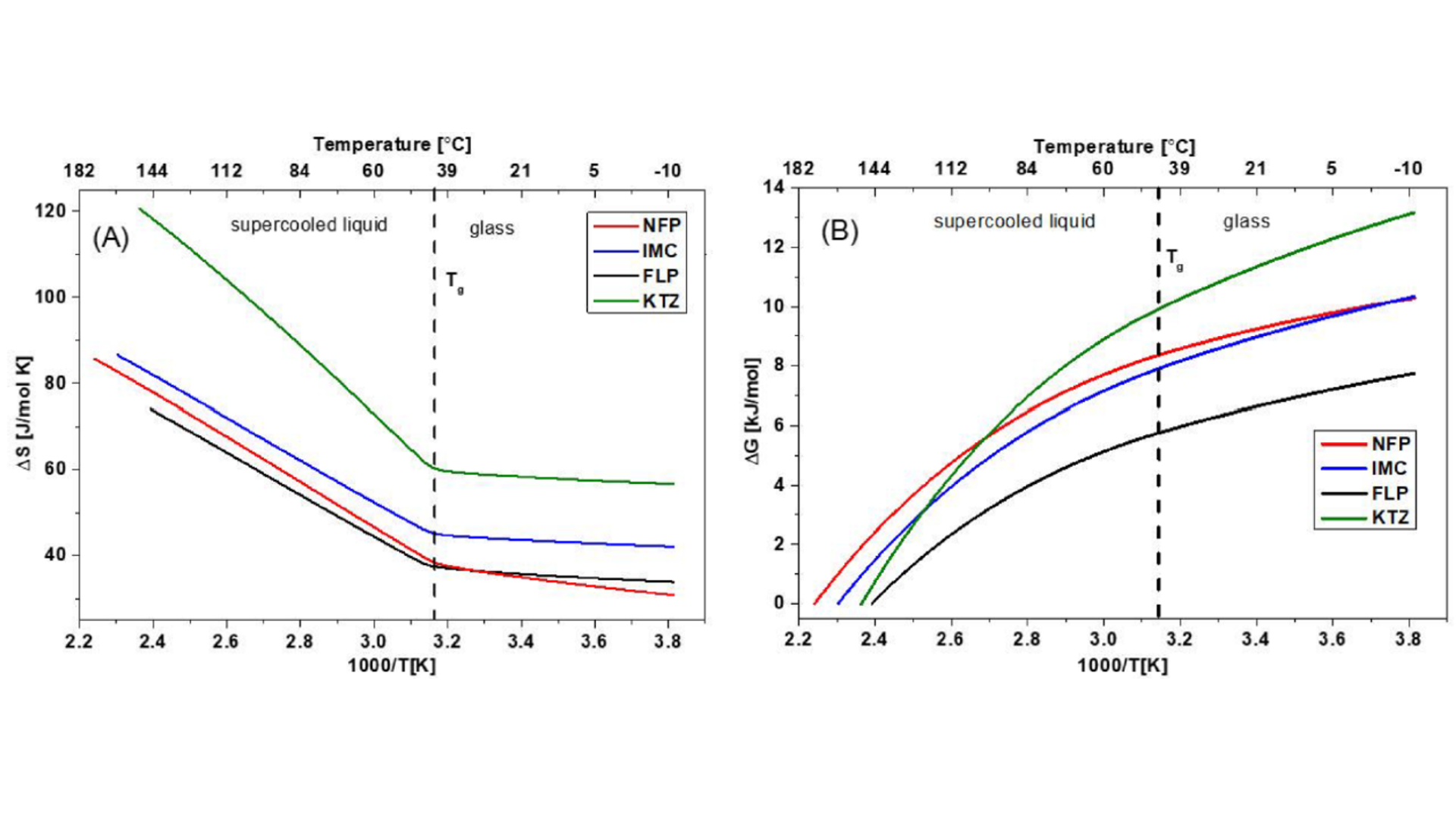
图 5 Difference in thermodynamic functions between the amorphous and the most stable crystalline state (polymorph) as a function of inverse temperature: (A) entropy (ΔS) and (B) Gibbs free energy (ΔG).
由于模型化合物的构型热力学函数值不同,它们在成核活化能垒上表现出明显的差异。由于相似的分子迁移率,成核活化能垒转化为低结晶倾向。(TΔS)3/ΔG2值越高的化合物稳定性越高,可按照NFP < IMC < FLP < KTZ排序,且与无定型化合物的结晶倾向排序相吻合。
05 模型化合物的热力学能垒和结晶倾向
利用热活化模型评估TTT结果得到活化能垒。活化模型与实验τ0(T)数据的非线性最小二乘拟合给出了比例常数N和B。在所有模型化合物中,成核活化能随温度的增加而增加。四种模型化合物在任意温度下的结晶诱导时间与其活化能成正比。
结晶活化能可以用来表示每种化合物的结晶倾向。NFP在三种选定温度下的情况如图6所示。随着温度的升高,弛豫时间减小,跳跃频率有所增加。随着温度的升高,ΔG减小,表示非晶态和晶态之间的自由能差减小。同时化合物的熵差随温度增加,由此,活化能Ea(T) 随温度增加。因此TTT图是活化能增加和分子迁移率对温度函数的综合效应的结果。这意味着,热力学活化能垒与分子迁移率在决定结晶倾向方面共同起到了重要作用。
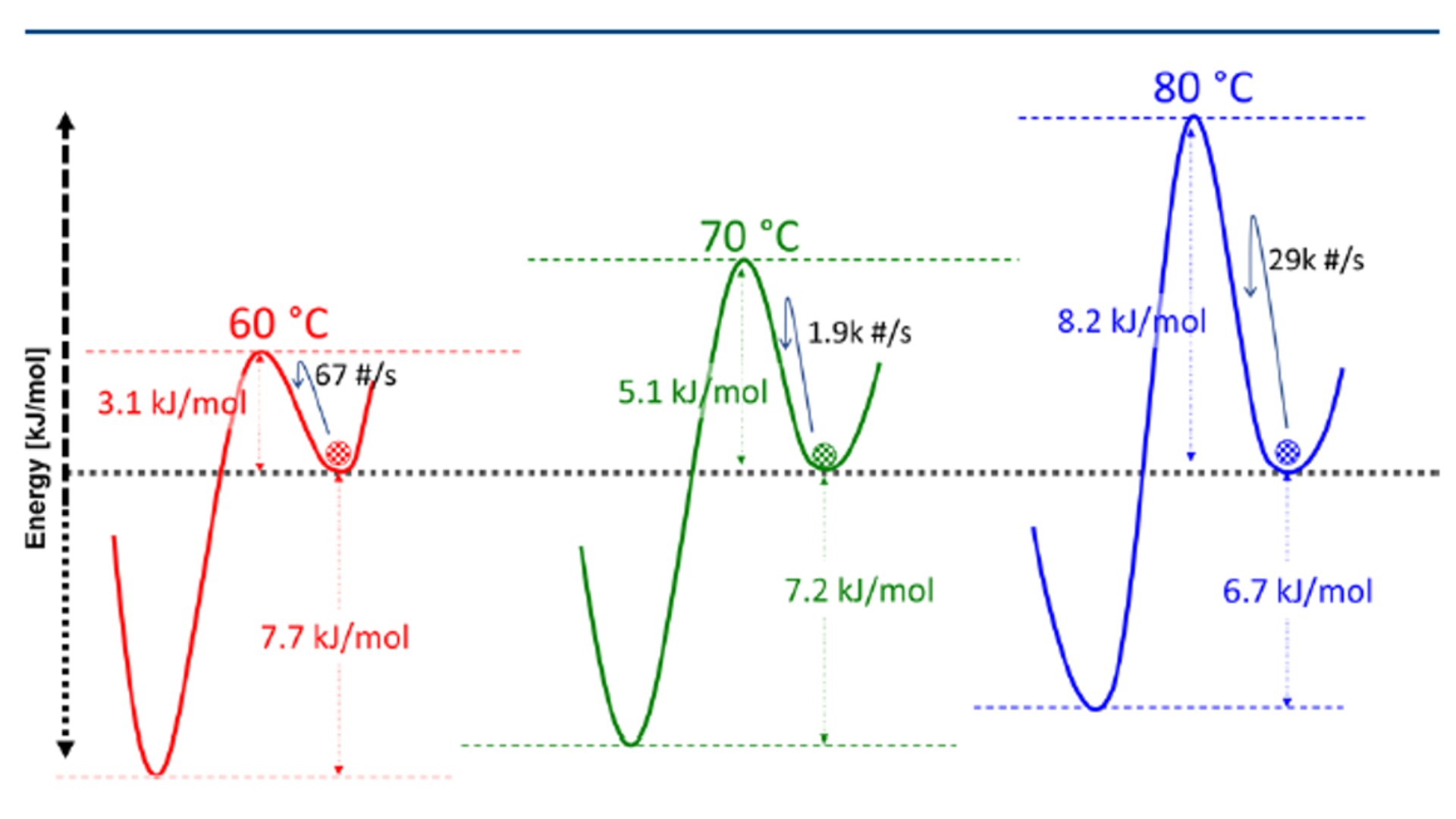
图 6 Schematic of the energy landscape of nifedipine at selected temperatures.
虽然模型化合物的分子迁移率在同一个数量级,但活化能的差异导致其结晶诱导时间的显著差异。由于活化能以指数方式影响成功跃迁的频率,因此活化能的微小变化将对结晶诱导时间产生相当大的影响。
本研究系统考察了四种Tg相近但结晶倾向差异显著的模型化合物,结合动力学和热力学因素来解释无定型药物的结晶行为。结晶诱导时间取决于“尝试跃迁”(动力学参数)和活化能势垒(热力学参数)。由于两种化合物具有相似的分子迁移率,因此结晶行为的显著差异可以用成核的热力学激活势垒来解释。